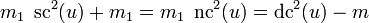Lt304888.ru

Туристические услуги

Эллиптические функции Якоби

13-10-2023

Эллиптические функции Якоби — это набор основных эллиптических функций комплексного переменного, и вспомогательных тэта-функций, которые имеют прямое отношение к некоторым прикладным задачам (например, уравнение маятника). Они также имеют полезные аналогии с тригонометрическими функциями, как показывает соответствующее обозначение для . Они не дают самый простой способ развить общую теорию, как замечено недавно: это может быть сказано на основе эллиптических функций Вейерштрасса. Эллиптические функции Якоби имеют в основном параллелограмме по два простых полюса и два простых нуля.

Содержание

Введение

Существует эллиптическая функция, имеющая в основном параллелограмме один полюс второго порядка и два простых нуля; это — «эллиптическая функция Вейерштрасса». Впрочем, более полезны «эллиптические функции Якоби», имеющие по два простых полюса и по два простых нуля в каждом основном параллелограмме. Каждая из этих функций в основном параллелограмме принимает любое значение в точности два раза.

Обозначение

Для эллиптических функций можно встретить разнообразные обозначения, которые могут запутать суть дела. Эллиптические функции — функции двух переменных. Первую переменную можно дать в терминах амплитуды φ, или обычно, в терминах u, данного ниже. Вторую переменную можно было бы дать в терминах параметра m, или как эллиптический модуль k, где k ² = m, или в терминах модулярного угла , где .

Определение как обратные к эллиптическим интегралам

Приведённое выше определение в терминах мероморфных функций абстрактно. Существует более простое, но абсолютно эквивалентное определение, задающее эллиптические функции как обратные к неполному эллиптическому интегралу первого рода. Это возможно наипростейшее определение для понимания. Пусть

Эллиптическая функция sn u задаётся как

и cn u определяется

а

Здесь угол называется амплитудой. называется дельта амплитудой. Значение m является свободным параметром, который полагается реальным в диапазоне , и таким образом эллиптические функции являются функциями двух аргументов: амплитуды и параметра m.

Оставшиеся девять эллиптических функций легко построить из трёх вышеприведённых. Это будет сделано ниже.

Заметьте, что когда , то u равен четверти периода K.

Определение в терминах тэта-функций

Эквивалентно эллиптические функции Якоби можно определить в терминах θ-функций. Если мы определим как , и соответственно как (тэта константы) тогда эллиптический модуль k равен . полагая , получим



Поскольку функции Якоби определяются в терминах эллиптического модуля , необходимо найти обратные к ним и выразить τ в терминах k. Начнём с дополнительного модуля . Как функция τ запишем

Введём обозначение

\ell = {1 \over 2} {1-\sqrt{k'} \over 1+\sqrt{k'}} = {1 \over 2} {\vartheta - \vartheta_{01} \over \vartheta + \vartheta_{01}}.

Определим также ном q как и разложим в ряд по степеням нома q. Получим

Обращение ряда даёт

Поскольку мы можем рассмотреть частный случай когда мнимая часть τ больше или равна , мы можем сказать, что значение q меньше или равно . Для таких малых значений вышеприведённый ряд сходится очень быстро, и это позволяет легко найти подходящее значение для q.

Другие функции

Изменением порядка двух букв в названии функций обычно обозначают обратные к трём функциям приведённых выше:

\operatorname{ns}(u)=1/\operatorname{sn}(u)
\operatorname{nc}(u)=1/\operatorname{cn}(u)
\operatorname{nd}(u)=1/\operatorname{dn}(u)

Отношения трех главных функций обозначают первой буквой числителя, следующей перед первой буквой знаменателя:

\operatorname{sc}(u)=\operatorname{sn}(u)/\operatorname{cn(u)}
\operatorname{sd}(u)=\operatorname{sn}(u)/\operatorname{dn(u)}
\operatorname{dc}(u)=\operatorname{dn}(u)/\operatorname{cn(u)}
\operatorname{ds}(u)=\operatorname{dn}(u)/\operatorname{sn(u)}
\operatorname{cs}(u)=\operatorname{cn}(u)/\operatorname{sn(u)}
\operatorname{cd}(u)=\operatorname{cn}(u)/\operatorname{dn(u)}

Более кратко запишем

где все буквы p, q, и r являются любыми буквами s, c, d, n (следует помнить, что ss = cc = dd = nn = 1).

Дополнительные теоремы

Функции удовлетворяют двум алгебраическим соотношениям

Видно, что (cn, sn, dn) параметризует эллиптическую кривую, которая является пересечением двух квадрик определенной вышеупомянутыми двумя уравнениями. Мы теперь можем определить групповой закон для точек на этой кривой с помощью дополнениятельных формул для функций Якоби

\operatorname{cn}(x+y) = {\operatorname{cn}(x)\;\operatorname{cn}(y) - \operatorname{sn}(x)\;\operatorname{sn}(y)\;\operatorname{dn}(x)\;\operatorname{dn}(y) \over {1 - k^2 \;\operatorname{sn}^2 (x) \;\operatorname{sn}^2 (y)}},


\operatorname{sn}(x+y) = {\operatorname{sn}(x)\;\operatorname{cn}(y)\;\operatorname{dn}(y) + \operatorname{sn}(y)\;\operatorname{cn}(x)\;\operatorname{dn}(x) \over {1 - k^2 \;\operatorname{sn}^2 (x)\; \operatorname{sn}^2 (y)}},


\operatorname{dn}(x+y) = {\operatorname{dn}(x)\;\operatorname{dn}(y) - k^2 \;\operatorname{sn}(x)\;\operatorname{sn}(y)\;\operatorname{cn}(x)\;\operatorname{cn}(y) \over {1 - k^2 \;\operatorname{sn}^2 (x)\; \operatorname{sn}^2 (y)}}.

Тригонометрические и гиперболические функции, как частный случай эллиптических

  • Если m = 1, то
;

Отсюда

Отсюда

и

Таким образом, при m = 1 эллиптические функции вырождаются в гиперболические.

  • Если m = 0, то
;

Отсюда

,

а также

,
,

Таким образом, при m = 0 эллиптические функции вырождаются в тригонометрические.

Соотношение между квадратами функций

Для квадратов этих функций верны следующие соотношения

-\operatorname{dn}^2(u)+m_1= -m\;\operatorname{cn}^2(u) = m\;\operatorname{sn}^2(u)-m
-m_1\;\operatorname{nd}^2(u)+m_1= -mm_1\;\operatorname{sd}^2(u) = m\;\operatorname{cd}^2(u)-m
m_1\;\operatorname{sc}^2(u)+m_1= m_1\;\operatorname{nc}^2(u) = \operatorname{dc}^2(u)-m
\operatorname{cs}^2(u)+m_1=\operatorname{ds}^2(u)=\operatorname{ns}^2(u)-m

где и .

Дополнительные равенства для квадратов можно получить если заметить, что , а также где p, q, r — любые буквы s, c, d, n и ss = cc = dd = nn = 1.

Ном

Пусть ном равен и пусть аргумент — . Тогда функции можно представить в виде сумм Ламберта

\operatorname{sn}(u)=\frac{2\pi}{K\sqrt{m}} \sum_{n=0}^\infty \frac{q^{n+1/2}}{1-q^{2n+1}} \sin (2n+1)v,
\operatorname{cn}(u)=\frac{2\pi}{K\sqrt{m}} \sum_{n=0}^\infty \frac{q^{n+1/2}}{1+q^{2n+1}} \cos (2n+1)v,
\operatorname{dn}(u)=\frac{\pi}{2K} + \frac{2\pi}{K} \sum_{n=1}^\infty \frac{q^{n}}{1+q^{2n}} \cos 2nv.

Решения нелинейных обыкновенных дифференциальных уравнений

Производные трёх основных эллиптических функций якоби записываются в виде:

\frac{\mathrm{d}}{\mathrm{d}z}\, \mathrm{sn}\,(z; k) = \mathrm{cn}\,(z;k)\, \mathrm{dn}\,(z;k),



\frac{\mathrm{d}}{\mathrm{d}z}\, \mathrm{dn}\,(z; k) = - k^2 \mathrm{sn}\,(z;k)\, \mathrm{cn}\,(z;k).

Используя теорему, формулировка которой приведена выше получим для заданного k (0 < k < 1) уравнения решениями которых являются эллиптические функции Якоби:

  • является решением уравнения и
  • является решением уравнения и
  • является решением уравнения и

Ссылки

  • Weisstein, Eric W. Jacobi Elliptic Functions (англ.) на сайте Wolfram MathWorld.
  • Эллиптические функции // Двайт Г. Б., Таблицы интегралов и другие математические формулы (MathML)
  • Эллиптические функции, Процедуры для Matlab

Литература

  • Abramowitz Milton Chapter 16
  • Н. И. Ахиезер Элементы теории эллиптических функций. — Москва: Наука, 1970.
  • Дж. Н. Ватсон Э. Т. Уиттекер Курс современного анализа. Ч.2. Трансцендентные функции. — Москва: Мир, 1963. или Москва: УРСС, 2010

Эллиптические функции Якоби.

© 2020–2023 lt304888.ru, Россия, Волжский, ул. Больничная 49, +7 (8443) 85-29-01